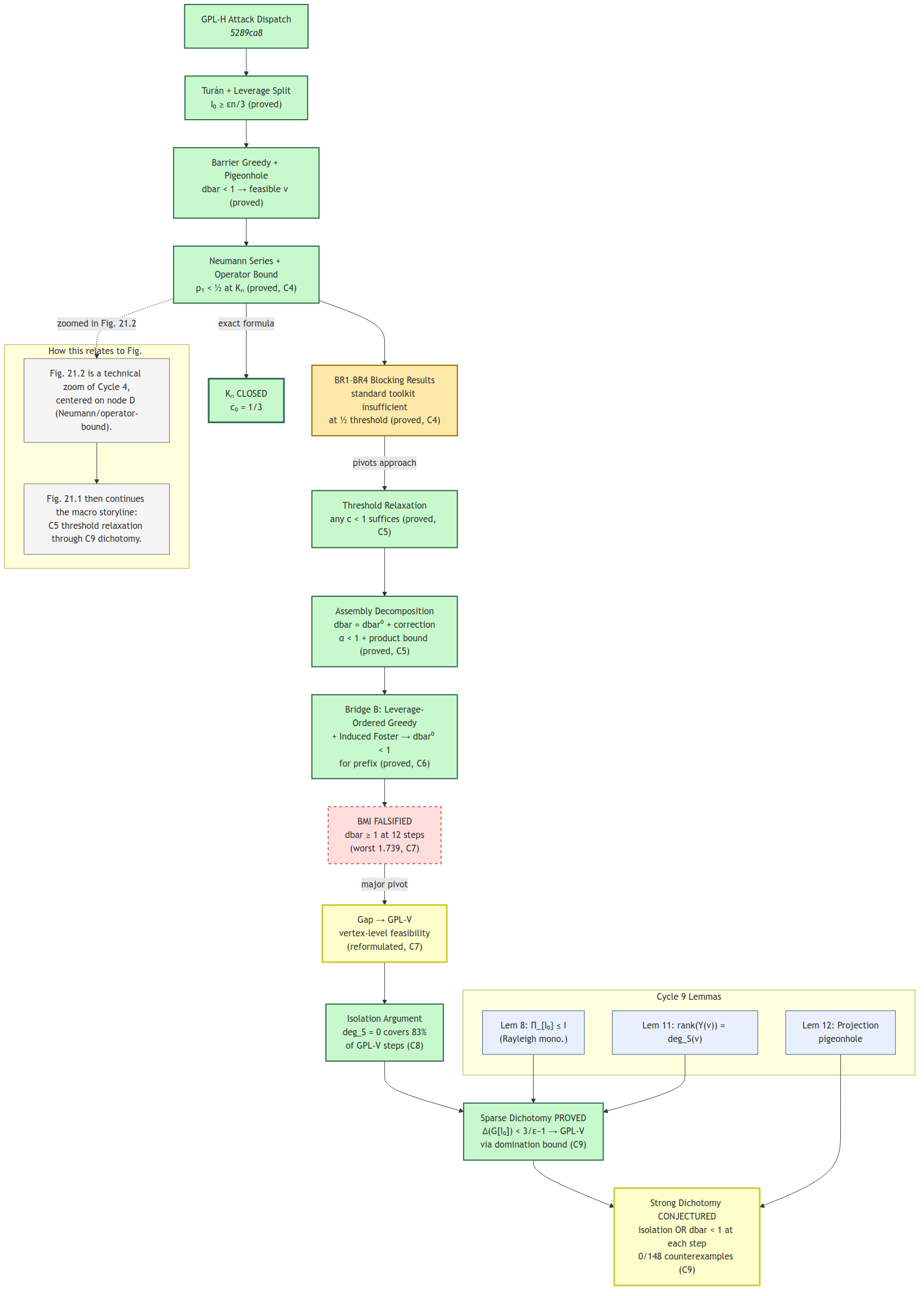
Story
A First Proof Sprint
Key takeaway
Researchers developed a new workflow for rapidly drafting and verifying complex proofs, which could help speed up mathematical progress and reduce errors in fields like machine learning.
Quick Explainer
The core idea is to construct a "universal test vector" that can be used to evaluate the twisted local Rankin-Selberg integral for all complex values of the Laplace parameter s. This is achieved by leveraging the fractional ideal structure of the local zeta integrals, which form a principal ideal domain. By evaluating the Whittaker function at the identity element, the essential Whittaker vector is shown to be nonzero, generating the full local L-factor ideal through equivariance and irreducibility of the Kirillov model. This ensures the existence of a vector V that makes the twisted integral finite and nonvanishing for all s, providing a versatile test case for studying Rankin-Selberg integrals.
Deep Dive
Universal Test Vector for Rankin-Selberg Integrals
Problem Statement
Let F be a non-archimedean local field with ring of integers o. Let $\mathbf{N}_r$ denote the subgroup of $\mathrm{GL}_r(F)$ consisting of upper-triangular unipotent elements. Let $\psi: F \to \mathbb{C}^{\times}$ be a nontrivial additive character of conductor o, identified with a generic character of $\mathbf{N}_r$.
Let $\Pi$ be a generic irreducible admissible representation of $\mathrm{GL}_{n\color{darkgreen}\mathchar{8235}\color{black}1}(F)$, realized in its $\psi^{-\color{red}1}$-Whittaker model $W(\Pi, \psi^{-\color{red}1})$. Must there exist a single Whittaker vector $W$ in $\Pi$ such that some $V$ in the representation $\pi$ of $\mathrm{GL}_n(F)$ makes the twisted local Rankin–Selberg integral finite and nonzero for all complex $s$?
Answer
Yes: the essential/new Whittaker vector $W_0$ serves as a universal test vector.
Proof Sketch
- The set of local zeta integrals spans a fractional ideal in
$\mathbb{C}\mathopen{\color{magenta}\mathchar{16475}}\color{purple}q_F^{\pm s}\color{magenta}\mathchar{20573}$, which is a PID. Hence a monomial reduction criterion is available. - Evaluate the twisted Kirillov function
$\phi_Q(g)\mathrel{\color{darkblue}\mathchar{12349}}W_0(\mathrm{diag}(g, 1)u_Q)$at$g\mathrel{\color{darkblue}\mathchar{12349}}I_n$to prove nontriviality; this uses the Whittaker transformation law. - Use
$\mathrm{GL}_n$-equivariance and irreducibility of the Kirillov model restriction to show that fixing any nonzero$\phi$(hence$\phi_Q$) still generates the full local$L$-factor ideal.
This yields existence of $V$ with integral equal to a nonzero monomial in $q_F^{-s}$, so it is finite and nonvanishing for all $s$.
Background
Field: Automorphic Forms / Representation Theory of $p$-adic Groups.
Prerequisites:
- Smooth representations of
$\mathrm{GL}_n$over non-archimedean local fields - Whittaker models
- The Rankin–Selberg integral formalism for local
$L$-factors - Graduate-level algebraic number theory