Story
VP-VAE: Rethinking Vector Quantization via Adaptive Vector Perturbation
Key takeaway
Researchers developed a new way to train generative models that is more stable and avoids common issues like "codebook collapse". This could lead to more reliable and higher-quality AI-generated content.
Quick Explainer
VP-VAE rethinks vector quantization by replacing the traditional non-differentiable quantization operator with a differentiable latent perturbation mechanism. This decouples representation learning from discrete codebook optimization, eliminating the training instability and codebook collapse issues often seen in standard VQ-VAE models. The key idea is to use Metropolis-Hastings sampling to inject structured perturbations into the latent space, aligning the perturbation magnitude with the expected quantization error and maintaining consistency with the original latent distribution. The authors also derive a simplified variant, FSP, that assumes a uniform latent distribution and uses a Lloyd-Max centroid-based quantization scheme. This decoupled approach enables VP-VAE and FSP to achieve superior reconstruction quality and codebook utilization compared to prior VQ-VAE methods.
Deep Dive
Technical Deep Dive: VP-VAE - Rethinking Vector Quantization via Adaptive Vector Perturbation
Overview
Vector Quantized Variational Autoencoders (VQ-VAEs) are a fundamental approach to learning discrete representations for generative modeling. However, VQ-VAEs often suffer from training instability and "codebook collapse" due to the coupling between representation learning and discrete codebook optimization.
This paper proposes VP-VAE, a new paradigm that decouples representation learning from discretization by eliminating the need for an explicit codebook during training. The key idea is to replace the non-differentiable quantizer with a distribution-consistent and scale-adaptive latent perturbation mechanism based on Metropolis-Hastings sampling. This allows the encoder-decoder to be trained without an explicit codebook, which is only generated after training convergence.
Additionally, under the assumption of approximately uniform latent variables, the authors derive FSP (Finite Scalar Perturbation), a lightweight variant of VP-VAE that aligns with principles of optimal scalar quantization.
Methodology
VP-VAE: From Quantization to Perturbation
VP-VAE replaces the discrete quantization operator with an explicit perturbation operator T that injects structured perturbations into the latent space:
- Scale Alignment: The perturbation magnitude is designed to match the expected quantization error implied by a target codebook size
K. - Distribution Consistency: Perturbed latent vectors
z̃are kept within high-density regions of the original latent distributionzusing Metropolis-Hastings sampling.
FSP: Finite Scalar Perturbation
When the latent distribution can be approximated as uniform, FSP provides a simplified perturbation and quantization scheme:
- Latent variables are constrained to the unit interval
[0, 1]^dusing a "CDF-like" activation function. - Perturbations are sampled uniformly within fixed intervals aligned with the expected quantization bin widths.
- Quantization uses Lloyd-Max centroids instead of rounding to grid boundaries.
Data & Experimental Setup
Experiments are conducted on image reconstruction (COCO, ImageNet) and audio compression (LibriSpeech, CommonVoice) tasks. Various codebook sizes (K ∈ {256, 1024, 4096, 16384}) are evaluated.
Key baselines include:
- VQ-VAE: The foundational coupled quantization approach.
- SimVQ: A state-of-the-art coupled method with learned codebook reparameterization.
- FSQ: A fixed scalar quantizer.
- TokenBridge: A predefined Gaussian grid discretization approach.
Evaluation metrics:
- Reconstruction quality: PSNR, SSIM, LPIPS (images), PESQ, STOI (audio)
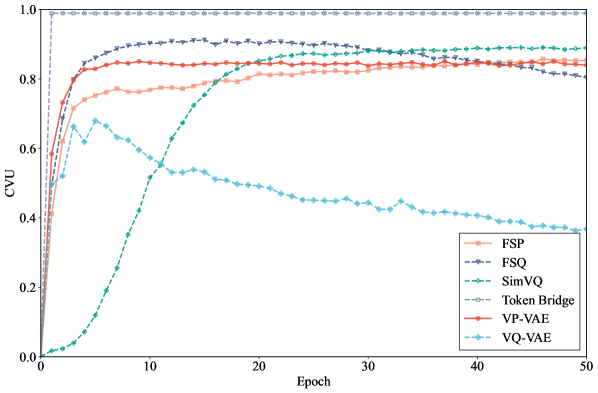
- Codebook utilization: Codebook Valid Usage (CVU) - a balanced usage metric.
Results
- VP-VAE and FSP consistently improve reconstruction fidelity while achieving higher and more balanced codebook utilization compared to baselines.
- The decoupled training paradigm of VP-VAE and FSP yields superior cross-modal stability and out-of-distribution generalization.
- FSP outperforms the rounding-based fixed quantizer FSQ, validating the benefits of the Lloyd-Max centroid-based perturbation and quantization.
Limitations & Uncertainties
- VP-VAE relies on non-parametric density estimation via k-nearest-neighbor search, which introduces computational overhead that could limit scalability to very large models.
- The current experiments focus on autoencoder-based tokenization; integrating VP-VAE with autoregressive or diffusion-based token generators remains an interesting future direction.
What Comes Next
The authors propose several promising research directions:
- Exploring techniques to further accelerate the non-parametric density estimation in VP-VAE, such as approximate nearest-neighbor search.
- Investigating the integration of VP-VAE with autoregressive or diffusion-based token generation models.
- Analyzing the theoretical properties and optimality of the FSP perturbation and quantization scheme under more general latent distributions.