AutoNumerics: An Autonomous, PDE-Agnostic Multi-Agent Pipeline for Scientific Computing

Technical Deep Dive: AutoNumerics

Overview

AutoNumerics is an autonomous, multi-agent framework that constructs transparent numerical solvers for partial differential equations (PDEs) directly from natural language problem descriptions. Unlike black-box neural network solvers, AutoNumerics generates interpretable classical numerical schemes grounded in numerical analysis principles.

The key innovations include:

• A coarse-to-fine execution strategy that decouples logic debugging from numerical stability validation.
• A residual-based self-verification mechanism that assesses solver quality without requiring analytical solutions.
• A reasoning module that detects and filters ill-designed or non-expert numerical plans.

Problem & Context

Solving PDEs is a central task in computational research, but traditional approaches require substantial expertise in numerical analysis. Recent neural network-based methods improve flexibility but often lack interpretability and incur high computational costs.

Large language models (LLMs) have shown promise in scientific code generation, but existing LLM-assisted PDE efforts either produce black-box networks, are constrained by fixed library APIs, or lack autonomous debugging and correctness verification.

Methodology

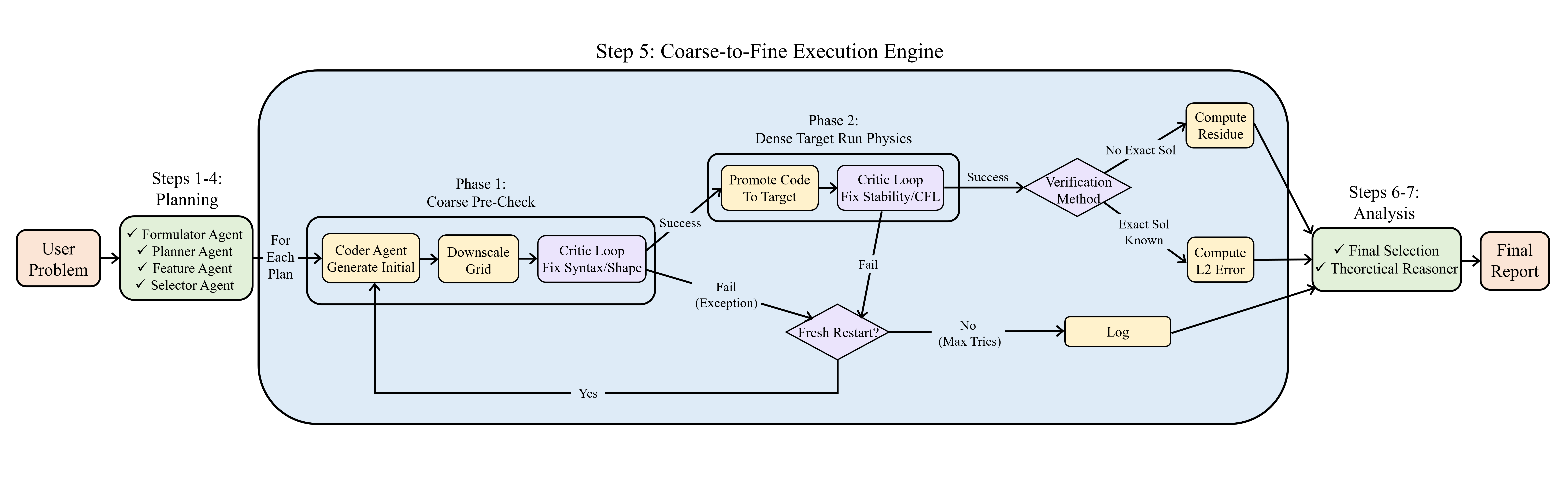
The AutoNumerics pipeline consists of several specialized agents coordinated by a central dispatcher:

1. The Formulator Agent converts natural language problem descriptions into structured PDE specifications.
2. The Planner Agent proposes multiple candidate numerical schemes, avoiding configurations that violate stability and consistency principles.
3. The Feature Agent extracts numerical properties from the problem and proposed schemes.
4. The Selector Agent scores and ranks the candidates, filtering out ill-designed plans.
5. The Coder Agent implements the selected schemes, using a coarse-to-fine execution strategy to decouple logic debugging from stability validation.
6. The Critic Agent fixes logic issues in the coarse-grid phase, and the Verifier Agent evaluates solver quality via residual-based self-verification.

Data & Experimental Setup

The authors evaluate AutoNumerics on two benchmark suites:

1. The CodePDE benchmark, comprising 5 representative PDEs: 1D Advection, 1D Burgers, 2D Reaction-Diffusion, 2D Compressible Navier-Stokes, and 2D Darcy Flow.
2. A larger in-house benchmark with 200 PDEs covering a wide range of common families (Advection, Burgers, Fokker-Planck, Heat, Maxwell, Poisson, etc.), spanning 1D to 5D and elliptic, parabolic, and hyperbolic types.

The Planner Agent generates 10 candidate schemes per problem, and the top 5 are passed to the Coder Agent for implementation and evaluation.

Results

On the CodePDE benchmark, AutoNumerics achieves the lowest normalized root mean square error (nRMSE) across all 5 problems, outperforming both neural network baselines and the CodePDE framework by approximately 6 orders of magnitude.

Out of 24 representative problems selected from the larger 200-PDE benchmark:

• 11 achieve relative L₂ errors of 10⁻⁶ or better, with Poisson and Helmholtz 2D reaching near machine precision.
• The system struggles with high-dimensional (≥5D) and high-order PDEs, such as Biharmonic and 5D Helmholtz.
• Across all problems, the Planner Agent consistently selects numerical schemes (spectral for periodic domains, finite differences for Dirichlet boundaries, etc.) that align with the PDE's structural properties.

Interpretation

The Planner and Selector agents' stability-aware reasoning enables AutoNumerics to detect and exclude ill-designed or non-physical solver configurations before execution. The coarse-to-fine strategy and residual-based verification then allow the system to construct and validate high-quality solvers without requiring analytical solutions.

The framework's strong performance on the CodePDE benchmark and its ability to select appropriate numerical schemes suggest its viability as an accessible paradigm for automated PDE solving. However, limitations remain in handling high-dimensional and high-order PDEs.

Limitations & Uncertainties

• The system is coupled to a single LLM (GPT-4.1) and the generated code lacks formal convergence or stability guarantees.
• Evaluation is limited to regular domains; irregular geometries are not considered.
• Accuracy degrades for high-dimensional (≥5D) and high-order PDEs.

What Comes Next

Future work could explore:

• Integrating the system with verified numerical libraries to provide formal guarantees.
• Extending the framework to irregular domains and unstructured meshes.
• Improving performance on high-dimensional and high-order PDEs, perhaps through hybrid neural-classical approaches.
• Expanding the scope beyond PDEs to other classes of differential equations.