Conjugate Learning Theory: Uncovering the Mechanisms of Trainability and Generalization in Deep Neural Networks

Conjugate Learning Theory: Uncovering the Mechanisms of Trainability and Generalization in Deep Neural Networks

Overview

This work proposes the conjugate learning theory framework to systematically analyze the optimization dynamics and generalization mechanisms that underpin the performance of deep neural networks (DNNs) in practical learning scenarios.

The key contributions are:

• A unified framework for modeling diverse learning tasks (classification, regression, generative modeling) using convex conjugate duality
• Establishing that Fenchel-Young losses are the unique admissible form of the loss function under mild regularity conditions
• Introducing a novel structure matrix to characterize the trainability of DNNs and prove an equivalence between optimization of the empirical risk and control of the structure matrix's extremal eigenvalues
• Deriving both deterministic and probabilistic bounds on generalization error based on generalized conditional entropy
• Validating the theoretical predictions through extensive experiments on benchmark datasets and standard DNN architectures

Methodology

Practical Learnability and Exponential Families

• Only distributions in the exponential family are practically learnable from finite samples using parametric models
• Exponential families possess finite-dimensional sufficient statistics, enabling consistent estimation from limited data
• Non-exponential family distributions can be effectively approximated by discrete distributions with finite support

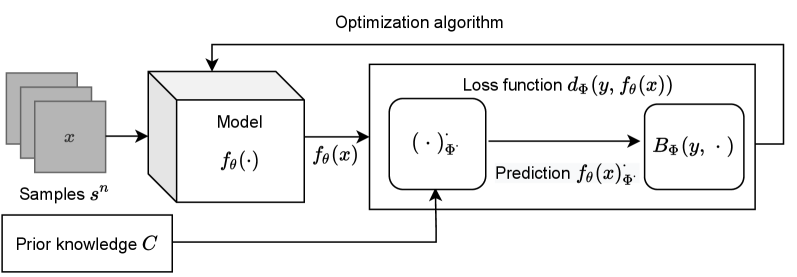
Conjugate Learning Framework

• Formalizes learning tasks as conditional distribution estimation problems
• Integrates domain-specific prior knowledge as convex constraints
• Uses the Fenchel-Young loss, which is the unique admissible form under mild regularity conditions
• Relaxes the i.i.d. assumption and allows for non-i.i.d. data distributions

Trainability Analysis

• Introduces the structure matrix to characterize the spectral properties of the model
• Proves an equivalence between empirical risk minimization and joint control of gradient energy and structure matrix eigenvalues
• Analyzes how mini-batch SGD minimizes gradient energy, with batch size, learning rate, and model architecture as key factors
• Demonstrates that skip connections and overparameterization preserve the conditioning of the structure matrix

Generalization Analysis

• Derives deterministic bounds on generalization error in terms of model maximum loss, information loss, and data conditional entropy
• Develops probabilistic bounds under i.i.d. sampling, relating sample size, distribution smoothness, and information loss to generalization
• Links parameter norm regularization to the control of the maximum loss

Data & Experimental Setup

• Datasets: MNIST, Fashion-MNIST, CIFAR-10, CIFAR-100, and reduced-scale versions (mini CIFAR-10 and mini CIFAR-100)
• Custom-designed models (Model A and Model B) and standard architectures (LeNet, ResNet18, Vision Transformer)
• Softmax cross entropy loss and MSE loss
• Disable techniques like Batch Normalization and Dropout to ensure consistent behavior between training and inference

Results

Trainability Validation

• The empirical risk is tightly bounded by the gradient energy and the extremal eigenvalues of the structure matrix
• Mini-batch SGD effectively minimizes gradient energy, with smaller batch sizes and sparser architectures leading to tighter control
• Skip connections and overparameterization preserve the conditioning of the structure matrix, maintaining trainability

Generalization Validation

• Deterministic bounds accurately capture the feasible range of generalization error for different models and datasets
• Probabilistic bounds quantify how sample size, information loss, and distributional smoothness affect the likelihood of small generalization error
• L2 regularization reduces the maximum loss, tightening both deterministic and probabilistic generalization bounds

Interpretation

• Conjugate learning theory provides a unified framework that systematically analyzes the trainability and generalization mechanisms of DNNs
• Trainability is enabled by the joint minimization of gradient energy and control of the structure matrix's spectral properties
• Generalization is governed by the model's maximum loss, information loss, and the dataset's intrinsic uncertainty (generalized conditional entropy)
• Information-theoretic metrics like maximum loss and information loss offer theoretically grounded alternatives to traditional test-set based evaluation

Limitations & Uncertainties

• The Gradient Approximate Independence (GAI) assumption, while useful for analyzing overparameterization, is an idealized simplification of real DNN gradients
• The theoretical analysis assumes perfect model optimization (convergence to the global minimum), which may not hold in practice due to factors like numerical precision and gradient noise
• The framework focuses on single-task learning and does not explicitly address transfer learning or multi-task generalization

What Comes Next

• Extending the conjugate learning framework to handle more complex data distributions, such as those encountered in domains like natural language processing and reinforcement learning
• Exploring the implications of conjugate learning theory for the design of novel architectures, optimization algorithms, and regularization techniques
• Investigating the connections between conjugate learning and other emerging theoretical frameworks, such as the neural tangent kernel and information bottleneck, to develop a more comprehensive understanding of deep learning.