Story
TIFO: Time-Invariant Frequency Operator for Stationarity-Aware Representation Learning in Time Series
Key takeaway
A new technique called TIFO helps make time series forecasting more accurate by accounting for changes in the underlying data patterns over time. This could improve predictions in fields like finance, weather, and healthcare where data varies unpredictably.
Quick Explainer
The core idea of TIFO is to mitigate the distribution shift problem in time series forecasting by learning stationarity-aware weights in the frequency domain. TIFO has a two-stage process: First, it measures the stationarity of frequency components across the training dataset. Then, for each input sample, it applies dynamic frequency weighting based on the learned stationarity scores to emphasize stationary components and suppress non-stationary ones. This frequency-domain approach is distinctive as it directly models the underlying time-evolving structure of the time series, going beyond normalization-based techniques that only consider low-order statistics or heuristic frequency selection.
Deep Dive
TIFO: Time-Invariant Frequency Operator for Stationarity-Aware Representation Learning in Time Series
Overview
- Proposed a novel framework called Time-Invariant Frequency Operator (TIFO) to mitigate the distribution shift issue in time series forecasting
- TIFO learns stationarity-aware weights over the frequency spectrum across the entire dataset, highlighting stationary frequency components while suppressing non-stationary ones
- Extensive experiments demonstrate TIFO achieves superior performance, yielding 18 top-1 and 6 top-2 results out of 28 settings compared to baselines
Problem & Context
- Nonstationary time series forecasting suffers from distribution shift due to different distributions in training and test data
- Existing normalization-based methods fail to capture the underlying time-evolving structure across samples and do not model the complex time structure
- This paper proposes to address distributional shift by working in the frequency space and considering all possible time conditions
Methodology
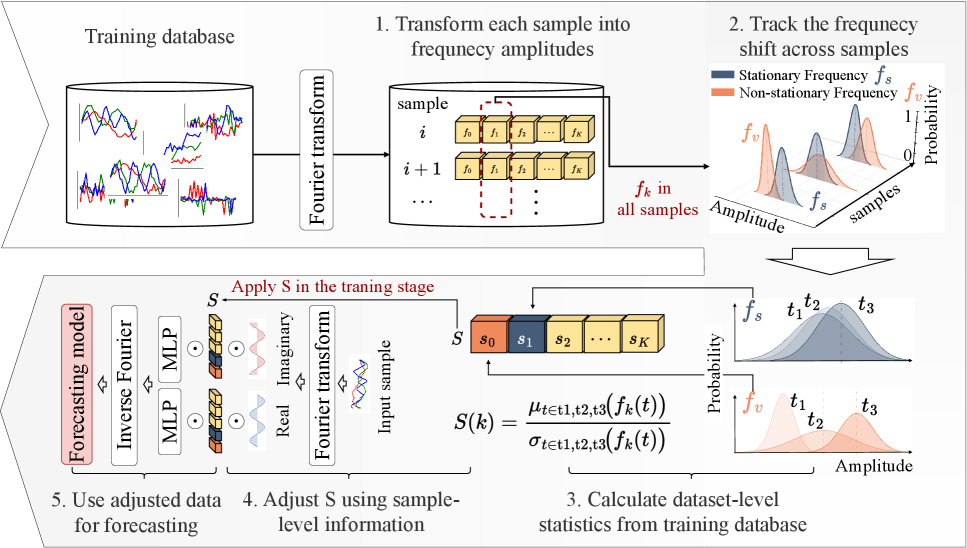
TIFO: System Overview and FeedForward Pipeline
TIFO has a two-stage modeling process:
- Dataset-level Stationarity Learning:
- Apply DFT to training samples to obtain amplitudes
- Measure frequency stationarity using mean/std across samples
- Save the stationarity scores $\mathbf{S}$ to be used in stage 2
- Sample-specific Learning & Forecasting:
- For each input sample, compute DFT and obtain real/imaginary coefficients
- Use MLPs to generate frequency weights $\boldsymbol{\lambda}r, \boldsymbol{\lambda}i$ based on $\mathbf{S}$
- Apply element-wise weighting to the coefficients
- Inverse DFT to transform back to time domain
- Feed the weighted time series into the forecasting model
Theoretical Analysis
- Leverages Bochner's and Mercer's theorems to show the existence of a time-averaged frequency representation and how learning the eigenvalues of this representation corresponds to learning the kernel itself
Data & Experimental Setup
- Benchmark on 7 multivariate time series datasets: Electricity Transformer Temperature (ETT), Electricity, Traffic, and Weather
- Compared against normalization-based baselines: RevIN, SAN, FAN
- Utilized DLinear, PatchTST, and iTransformer as the backbone forecasting models
Results
- TIFO consistently improves forecasting performance of the backbone models across all datasets
- Achieves 18 top-1 and 6 top-2 results out of 28 settings, with up to 33.3% and 55.3% improvements on ETTm2
- Significantly reduces the train-test distributional discrepancy in the frequency domain, as measured by JSD² and KS statistics
Interpretation
- TIFO's frequency-domain weighting effectively mitigates distribution shift by emphasizing stationary components and suppressing non-stationary ones
- Theoretically justified by showing TIFO learns the eigenvalues of the frequency-domain kernel, capturing the underlying time-evolving structure
- Outperforms normalization-based baselines that only consider low-order statistics or heuristic frequency selection
Limitations & Uncertainties
- The theoretical analysis assumes the training set sufficiently represents the underlying time-evolving distribution, which may not always hold in practice
- The effectiveness of TIFO could be sensitive to the choice of FFT-related hyperparameters, though experiments suggest it is reasonably robust
What Comes Next
- Explore online/adaptive updating of the frequency weights to handle distribution drift over time
- Investigate the interplay between TIFO and other frequency-domain modeling techniques for further performance gains
- Apply TIFO to related time series tasks beyond forecasting, such as anomaly detection and multivariate imputation