Genetic Generalized Additive Models

Technical Deep Dive: Genetic Generalized Additive Models

Overview

This paper proposes using the multi-objective genetic algorithm NSGA-II to automatically optimize the structure and hyperparameters of Generalized Additive Models (GAMs), enabling the discovery of accurate yet interpretable models. GAMs are a class of transparent models that decompose predictions into a sum of smooth, univariate functions. However, manually configuring the structure of GAMs to balance predictive performance and interpretability is challenging.

Methodology

• The researchers used NSGA-II to evolve GAM structures, encoding the type of term (none, linear, spline), number of spline basis functions, smoothing parameter λ, and feature scaling as genes in the GA chromosomes.
• NSGA-II optimized two objectives: 1) minimizing RMSE for predictive accuracy, and 2) minimizing a complexity penalty that captured model sparsity and uncertainty.
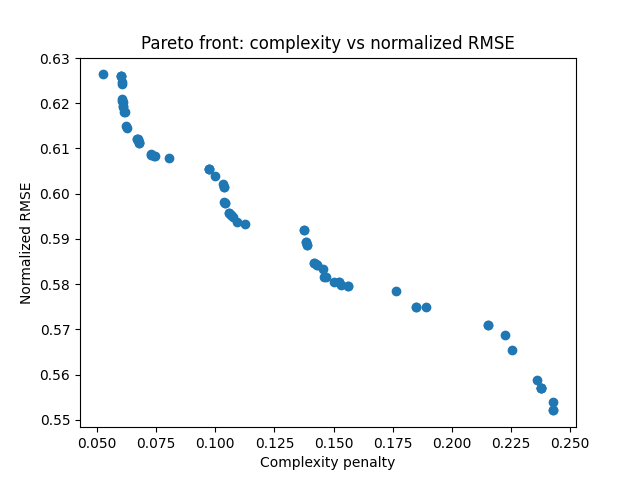
• The GA was run for 50 generations on the California Housing dataset, and three representative Pareto-optimal models were extracted: the RMSE-optimal, complexity-optimal, and knee-point solutions.

Results

• The GA-optimized GAMs consistently outperformed or matched the baseline LinearGAM and Decision Tree models in predictive accuracy, while exhibiting substantially lower complexity as measured by the penalty function.
• The RMSE-optimal GA model was simpler than the baseline LinearGAM despite achieving better predictive performance across all seeds.
• The complexity-optimal GA model remained competitive with the baselines in RMSE while attaining the lowest complexity penalty scores.
• Visualizations of the Pareto fronts demonstrated the diverse set of accuracy-complexity trade-offs discovered by NSGA-II.
• The GA-optimized GAMs produced simpler, smoother feature contributions with wider, more honest confidence intervals compared to the baseline LinearGAM.

Interpretation

• The results show that NSGA-II can effectively discover GAM structures that balance predictive accuracy and interpretability, without requiring manual specification of the model form.
• By jointly optimizing for low RMSE and low complexity, NSGA-II identifies models that achieve strong predictive performance while maintaining favorable structural properties like sparsity and smooth, informative feature contributions.
• The Pareto front of solutions provides a range of models that can be selected based on the specific needs and constraints of the application domain, rather than relying on accuracy alone.

Limitations and Uncertainties

• The paper only evaluates the proposed approach on a single dataset (California Housing), so the generalization to other problem domains is unclear.
• The computational cost of running NSGA-II was not quantified, and methods to reduce this cost (e.g., caching, memoization) were not explored.
• The study did not compare the NSGA-II-optimized GAMs to other interpretable model classes, such as fuzzy systems or rule-based models, which may exhibit different accuracy-complexity trade-offs.

Future Work

• Extend the multi-objective optimization approach to the design of fuzzy and cascading rule-based models, which share similar goals of balancing predictive performance and interpretability.
• Investigate strategies to reduce the computational cost of evaluating candidate models, such as caching or memoization, to enable large-scale multi-objective optimization of interpretable model structures.