Randomness and signal propagation in physics-informed neural networks (PINNs): A neural PDE perspective

Technical Deep Dive: Randomness and Signal Propagation in Physics-Informed Neural Networks (PINNs)

Overview

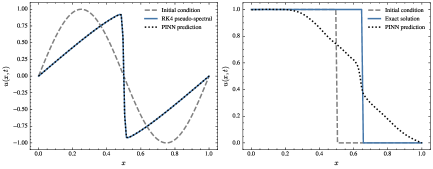
This work examines the statistical and spectral properties of trained weight matrices in physics-informed neural networks (PINNs), focusing on the viscous and inviscid variants of the 1D Burgers' equation. The authors find that the learned weights tend to reside in a high-entropy regime consistent with predictions from random matrix theory, raising questions about the interpretability and physical grounding of such networks. They then investigate how these random and structured weight matrices influence the stability of signal propagation through the lens of neural partial differential equations (PDEs).

Methodology

• Trained PINNs on viscous and inviscid Burgers' equation using 9 hidden layers with 100 neurons each and tanh activation.
• Analyzed the weight distributions using kernel density estimation and maximum likelihood estimation of generalized Gaussian fits.
• Performed spectral analysis of the weight matrices, comparing eigenvalue and singular value distributions to random matrix theory predictions.
• Modeled signal propagation through the network using a diagonally dominant random Gaussian kernel and observed instability in the evolution of input features.
• Interpreted the weight structures through the neural PDE framework, showing that numerical stability of the underlying discretized PDEs governs the reliability of signal propagation.

Results

• For the viscous Burgers' equation, the learned weights follow generalized Gaussian distributions, consistent with random matrix theory predictions.
• For the inviscid Burgers' equation, the weight distributions exhibit heavier tails, suggesting the presence of internal correlations and deviations from randomness, especially in the early and middle layers.
• Spectral analysis shows that the eigenvalue and singular value distributions of the weight matrices broadly agree with random matrix theory, with some deviations, particularly for the inviscid case.
• Signal propagation through the network exhibits instability and divergence, which the authors link to the numerical stability properties of the underlying neural PDEs implemented by the architecture.
• Stable implicit and higher-order numerical schemes for the neural PDEs lead to well-behaved signal dynamics, in contrast with the unstable explicit discretizations inherent in the standard PINN architecture.

Interpretation

• The authors suggest that the inherent randomness in the learned PINN weights, especially for the inviscid Burgers' equation, raises questions about the physical interpretability and insight provided by such models.
• They speculate that PINNs may represent a generalized path integral solution of the underlying PDEs, but note that further research is needed to establish this connection.
• The neural PDE framework provides a useful perspective for understanding signal propagation in deep networks, highlighting the importance of numerical stability properties in governing network dynamics.

Limitations and Uncertainties

• The analysis is limited to the 1D Burgers' equation and may not generalize to other PDE systems or PINN architectures.
• The authors do not provide a complete theoretical explanation for the observed deviations from random matrix theory, especially in the inviscid case.
• The link between weight statistics, neural PDE discretizations, and physical interpretability remains speculative and requires further investigation.

Future Work

• Explore the connection between PINNs and path integral formulations of PDEs in more detail.
• Investigate the influence of network architecture, activation functions, and other design choices on the weight statistics and numerical stability properties.
• Extend the analysis to a wider range of PDE systems and more complex PINN architectures.
• Develop principled frameworks for designing PINN architectures that better preserve the underlying physical structure and dynamics.

Sources:

• Randomness and signal propagation in physics-informed neural networks (PINNs): A neural PDE perspective