Dataless Weight Disentanglement in Task Arithmetic via Kronecker-Factored Approximate Curvature

Technical Deep Dive: Dataless Weight Disentanglement in Task Arithmetic via Kronecker-Factored Approximate Curvature

Overview

This work addresses the problem of cross-task interference when composing multiple task vectors in Task Arithmetic (TA), a modular approach for adapting foundation models. The authors propose a dataless regularization technique called TAK that leverages Kronecker-Factored Approximate Curvature (KFAC) to encourage weight disentanglement and improve the performance of TA.

Problem & Context

• Task Arithmetic (TA) enables adapting foundation models by combining task-specific parameter updates (task vectors), but this can lead to cross-task interference and representation drift.
• Existing representation drift regularization approaches require access to external task data, which conflicts with modularity and data availability constraints.

Methodology

• The authors derive a dataless regularization objective by connecting representation drift to the Jacobian's Gram matrix, which can be approximated using the Generalized Gauss-Newton (GGN) matrix.
• They adopt the Kronecker-Factored Approximate Curvature (KFAC) method to efficiently approximate the GGN, enabling constant-complexity regularization regardless of the number of tasks.
• They propose an aggregation scheme to merge per-task curvature factors into a single surrogate, further improving efficiency.

Data & Experimental Setup

• Experiments are conducted on the 8 Vision benchmark, using CLIP as the foundational vision backbone.
• The authors evaluate both the linearized fine-tuning regime (as per Ortiz-Jimenez et al., 2023) and the standard non-linear fine-tuning.
• They compare their TAK method to baselines like linear fine-tuning, representation drift regularization (Yoshida et al., 2025), and diagonal GGN (Porrello et al., 2025).

Results

• In the linearized fine-tuning regime, TAK achieves state-of-the-art performance, outperforming baselines on both absolute and normalized accuracy metrics.
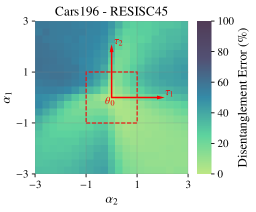
• TAK also exhibits desirable properties like task localization (distinct task vectors govern separate regions in function space) and robustness to task vector rescaling.
• In the non-linear fine-tuning regime, TAK significantly outperforms standard fine-tuning and attention-only fine-tuning (Jin et al., 2025).

Interpretation

• The authors' dataless regularization approach successfully addresses the cross-task interference problem in TA, enabling effective composition of task vectors without requiring access to external task data.
• The KFAC-based approximation provides an efficient and scalable solution, making the regularization practical for real-world applications with many tasks.

Limitations & Uncertainties

• The work is based on a preprint and has not yet been peer-reviewed or published.
• The experiments are limited to the 8 Vision benchmark and CLIP model. Broader evaluation across different domains and architectures would help validate the generalization of the proposed method.
• The authors do not discuss the computational overhead or runtime impact of their KFAC-based regularization, which could be an important practical consideration.

What Comes Next

• Further research could explore extending the dataless regularization approach to other types of foundation models beyond computer vision, such as language models or multimodal models.
• Investigating the interplay between the proposed regularization and other TA techniques, like fine-tuning order or task vector normalization, could yield additional insights.
• Exploring the role of the KFAC approximation quality and its impact on weight disentanglement and TA performance would be an interesting direction.

Sources:

• Dataless Weight Disentanglement in Task Arithmetic via Kronecker-Factored Approximate Curvature