Story
In-Context Learning in Linear vs. Quadratic Attention Models: An Empirical Study on Regression Tasks
Key takeaway
A new study found that transformer models with linear attention perform better at in-context learning for regression tasks compared to quadratic attention models.
Quick Explainer
This study explores how the choice of attention mechanism - linear versus quadratic - affects a transformer model's ability to adapt and learn new functions from just a few examples provided in the input context. The core idea is that the attention formulation, which determines how the model aggregates information across its layers, plays a key role in enabling this in-context learning capability. At a high level, the authors find that while both linear and quadratic attention can support effective in-context learning, the linear attention model converges faster to its final performance, suggesting this architectural choice may be less critical than ensuring sufficient model depth for robust adaptation.
Deep Dive
Technical Deep Dive: In-Context Learning in Linear vs. Quadratic Attention Models
Overview
This paper provides an empirical comparison of linear and quadratic attention mechanisms in their ability to perform in-context learning (ICL) on linear regression tasks. The authors evaluate the models' final performance, convergence behavior, and robustness to distribution shifts.
Problem & Context
- Recent work has shown that transformers can perform ICL - adapting to learn new functions from just a few examples provided in the input context.
- Prior research has provided mechanistic explanations for how ICL emerges from the transformer's internal computations, relating it to gradient-based meta-learning.
- This paper aims to understand how the choice of attention mechanism (linear vs. quadratic) affects ICL capabilities.
Methodology
- Task: Linear regression with 5-dimensional inputs, where the goal is to learn a new linear function from a few examples in the prompt.
- Models:
- Quadratic attention transformers (4-head GPT-2 style)
- Linear attention transformers (custom causal architecture with squared ReLU feature map)
- Evaluated at 1, 3, and 6 layer depths
- Training and evaluation:
- Squared error loss on predicting the final query target
- Tested on both isotropic and anisotropic input distributions
Results
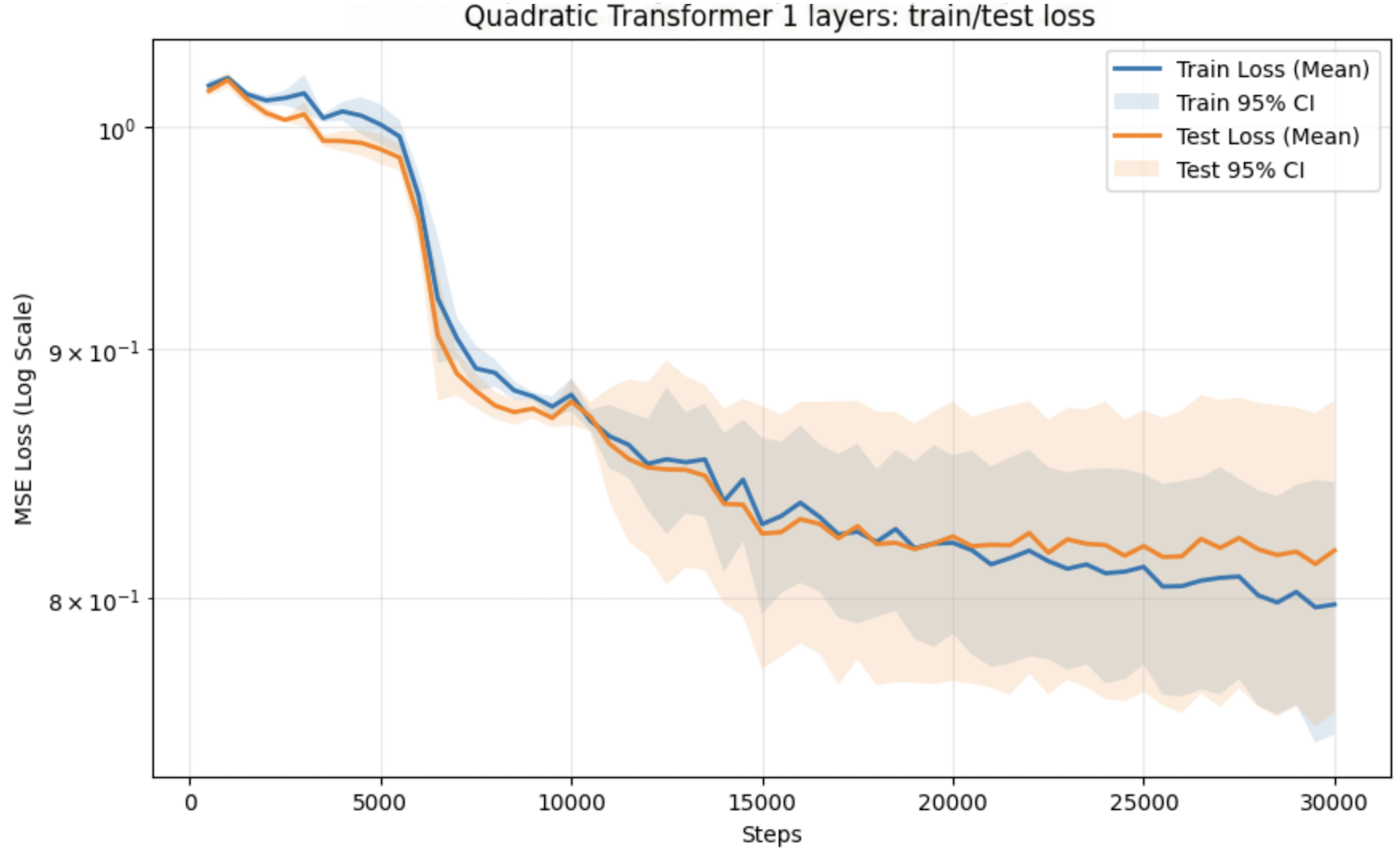
Convergence
- Linear attention models converge 1.6x faster than quadratic attention, reaching 90% of final performance in 256k-480k samples vs 688k-800k.
- Linear attention exhibits sharp initial drops in test loss before plateauing, while quadratic attention shows slower, more gradual convergence.
Depth Scaling
- Increasing depth from 1 to 6 layers dramatically improves performance for both architectures.
- 6-layer linear attention (0.0302 test loss) slightly outperforms 6-layer quadratic attention (0.0365).
- Single-layer models struggle, suggesting insufficient depth to implement the iterative refinement needed for robust ICL.
Robustness to Distribution Shifts
- Both architectures show reasonable robustness to anisotropic distribution shifts, with <10% performance degradation.
- Quadratic attention maintains a slight edge in distribution robustness, particularly at shallower depths.
Interpretation
- The results suggest that linear attention can largely replicate the ICL capabilities of quadratic attention, with the main difference being convergence speed.
- Depth is a critical factor, with 6-layer models of both types achieving strong performance and generalization.
- The modest differences in final performance and distribution robustness indicate that the choice of attention mechanism may be less important than architectural depth for ICL tasks.
Limitations & Uncertainties
- The analysis is limited to linear regression; more complex function classes could reveal starker differences in learning capabilities.
- The reasons for linear attention's faster convergence require further mechanistic investigation.
- Exploring hybrid architectures that combine linear and quadratic attention may uncover synergies.
What Comes Next
- Extending the analysis to other function classes and model types could provide a broader understanding of the architectural requirements for ICL.
- Investigating the specific mechanisms by which linear and quadratic attention implement gradient-based learning in-context could yield deeper theoretical insights.
- Exploring hybrid architectures that combine linear and quadratic attention may uncover synergies.