Tomography by Design: An Algebraic Approach to Low-Rank Quantum States

Technical Deep Dive: Tomography by Design

Overview

This paper presents an algebraic approach to quantum state tomography (QST) that leverages structured measurements to efficiently reconstruct low-rank quantum states. The key ideas are:

• Selective QST: Directly estimate a subset of density matrix entries using specialized measurement operators.
• Structured Matrix Completion: Use the observed submatrices to uniquely determine the full density matrix column space via standard numerical linear algebra.
• Deterministic Guarantees: Provide theoretical conditions for exact reconstruction under low-rank assumptions.

Problem & Context

Quantum state tomography is the task of reconstructing the density matrix $\bm{\rho}$ of a quantum system from measurements of various observables. This is challenging because:

1. $\bm{\rho}$ must satisfy physicality constraints (Hermitian, positive semidefinite, unit trace).
2. The number of measurements required to uniquely recover a full-rank $D \times D$ density matrix scales as $\mathcal{O}(D^2)$.

However, if the density matrix is known to be low-rank ($\text{rank}(\bm{\rho}) = R \ll D$), the measurement complexity can be reduced to $\mathcal{O}(RD \log^2 D)$.

Methodology

The proposed approach has two key stages:

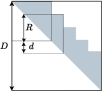
1. Measurement: Select a structured pattern of principal submatrices $\{\bm{\rho}^{(l)}_\text{obs}\}$ of the density matrix. These submatrices must satisfy an "isorank" property, meaning their rank equals the rank $R$ of the full matrix.
2. Reconstruction:
   • Use the observed submatrices to compute an orthonormal basis $\mathbf{U}$ that spans the column space of $\bm{\rho}$. This is done by finding the intersection of the subspaces induced by the observed submatrices.
   • Reconstruct the full density matrix $\bm{\rho}$ column-wise by solving least-squares problems, leveraging the fact that each column $\bm{\rho}{:c}$ can be expressed as $\bm{\rho}{:c} = \mathbf{U} \mathbf{x}$.

The authors provide deterministic guarantees for the uniqueness of this reconstruction process, which hold generically when the submatrices satisfy certain overlap and coverage conditions.

Data & Experimental Setup

The authors generate a random rank-2 density matrix for a 5-qubit system, and add Gaussian noise to the measurements with a signal-to-noise ratio of 30 dB.

They compare their proposed algebraic approach against two state-of-the-art methods:

1. Convex optimization (CVX): Solves the nuclear-norm minimization problem in Eq. (1).
2. Burer-Monteiro (BM) factorization: Solves the relaxed SDP in Eq. (2) via second-order optimization.

All methods use the same number of measurements, equal to twice the unique off-diagonal entries plus the $D$ diagonal entries.

Results

The proposed algebraic approach outperforms both the CVX and BM methods in terms of reconstruction accuracy, as measured by fidelity and trace distance. Furthermore, the algebraic approach is computationally much faster.

The accuracy of the algebraic approach improves as the overlap $d$ between the observed submatrices increases, since this provides more independent constraints on the global column space.

Limitations & Uncertainties

• The paper focuses on the theoretical and numerical aspects of the proposed approach, but does not discuss practical implementation details, such as the design of the measurement circuits.
• The experimental evaluation is limited to a single 5-qubit system. More comprehensive testing on larger systems would be needed to fully assess the scalability and robustness of the method.
• The paper does not explore the potential benefits of combining the algebraic approach with shadow tomography, which could significantly improve the scalability of the measurement process.

What Comes Next

The authors note that future work will:

• Provide more detailed numerical experiments, including the use of shadow tomography for estimating the structured density matrix entries.
• Discuss practical, circuit-level implementations of the measurement stage.

Overall, this paper presents a promising algebraic approach to quantum state tomography that offers improved accuracy and efficiency compared to state-of-the-art methods, while providing deterministic recovery guarantees under low-rank assumptions.