Story
Towards Efficient Constraint Handling in Neural Solvers for Routing Problems
Key takeaway
Researchers developed a new method to help neural networks solve complex routing problems more efficiently, which could improve real-world applications like delivery logistics and transportation planning.
Quick Explainer
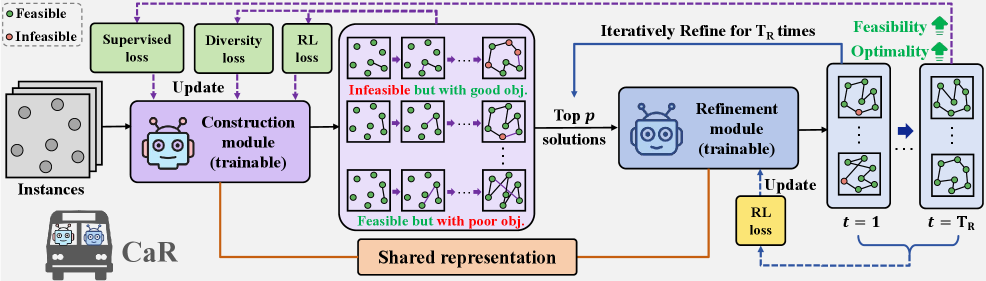
The Construct-and-Refine (CaR) framework takes a novel approach to handling constraints in neural solvers for routing problems. It jointly trains a construction module to generate diverse, high-quality initial solutions, and a lightweight refinement module to efficiently improve these solutions to satisfy complex real-world constraints. CaR leverages cross-paradigm representation learning, where a shared encoder enables knowledge transfer between the construction and refinement components, enhancing overall feasibility awareness. This explicit feasibility refinement scheme, combined with the joint training, allows CaR to outperform both classic and state-of-the-art neural solvers on routing problems with varying constraint complexities, demonstrating its effectiveness in advancing the applicability of neural combinatorial optimization methods.
Deep Dive
Technical Deep Dive: Towards Efficient Constraint Handling in Neural Solvers for Routing Problems
Overview
This technical deep dive summarizes the key contributions of the paper "Towards Efficient Constraint Handling in Neural Solvers for Routing Problems":
- Introduced Construct-and-Refine (CaR), a neural framework that handles constraints through an explicit feasibility refinement scheme, extending beyond feasibility masking and implicit feasibility awareness.
- CaR jointly learns to construct diverse, high-quality solutions and refine them with a lightweight improvement module, enabling efficient constraint satisfaction.
- Explored shared encoders for cross-paradigm representation learning to further enhance feasibility awareness.
- Demonstrated CaR's effectiveness on VRPs with varying constraint complexities, including TSPTW and CVRPBLTW, outperforming both classic and neural state-of-the-art solvers.
Problem & Context
- Vehicle Routing Problems (VRPs) often involve complex real-world constraints, such as capacity, time windows, and precedence constraints.
- Classic VRP solvers rely on carefully designed heuristics, while recent Neural Combinatorial Optimization (NCO) methods automate solver design with deep learning.
- However, NCO methods have primarily targeted simple VRP variants, leaving their potential on hard-constrained VRPs underexplored.
- Effective constraint handling remains a key challenge in advancing the broader applicability of NCO to real-world VRPs.
Methodology
Existing Constraint Handling Schemes
- Feasibility masking: Exclude invalid actions during solution construction or improvement. Becomes intractable for complex constraints.
- Implicit feasibility awareness: Enhance neural policies via reward/penalty-based guidance or feature augmentation. Still yields high infeasibility.
Construct-and-Refine (CaR) Framework
- Joint Training of Construction and Refinement:
- Construction module generates diverse, high-quality initial solutions.
- Refinement module rapidly enhances these solutions within a small number of steps (e.g., 10 steps).
- Supervised losses guide construction to produce solutions well-suited for refinement.
- Cross-Paradigm Representation Learning:
- Shared encoder to enable knowledge transfer between construction and refinement.
- Enhances feasibility awareness, particularly for complex constrained scenarios.
Data & Experimental Setup
- Evaluated on VRPs with varying constraint complexities:
- TSPTW: Complex constraints where feasibility masking is NP-hard.
- CVRPBLTW: Complex constraints where feasibility masking is tractable but ineffective.
- CVRP: Simple constraints where feasibility masking is tractable and effective.
- Compared to state-of-the-art classic and neural VRP solvers.
Results
- On TSPTW-50, CaR reduced infeasibility to 0.00% and achieved a minimal optimality gap of 0.005%, outperforming the best construction baseline PIP and the adapted state-of-the-art improvement solver NeuOpt*.
- On CVRPBLTW, CaR guaranteed 0% infeasibility while achieving superior solution quality and efficiency compared to both neural and classic solvers.
- CaR also delivered competitive performance on the simpler CVRP benchmark.
Interpretation
- CaR's explicit feasibility refinement scheme, combined with its cross-paradigm representation learning, enables effective constraint handling across a wide range of VRP complexities.
- The joint training of construction and refinement, with tailored losses, allows CaR to generate diverse, high-quality solutions that are well-suited for rapid improvement.
- The shared encoder facilitates knowledge transfer between the construction and refinement modules, particularly enhancing performance on complex constrained scenarios.
Limitations & Uncertainties
- While CaR demonstrates strong empirical performance, further theoretical analysis is needed to understand its learnability, convergence, and generalization properties.
- The current implementation assumes the user provides a valid working directory and does not handle errors or edge cases gracefully.
- Extending CaR to handle even broader classes of Combinatorial Optimization Problems (COPs), beyond VRPs, remains an open challenge.
What Comes Next
- Investigate the theoretical underpinnings of CaR, including its learnability, convergence guarantees, and generalization bounds.
- Explore ways to improve the robustness and error-handling capabilities of the framework.
- Apply the cross-paradigm representation learning insights from CaR to develop foundational NCO models that can be adapted to diverse COP domains.