Early-Warning Signals of Grokking via Loss-Landscape Geometry

Technical Deep Dive: Early-Warning Signals of Grokking via Loss-Landscape Geometry

Overview

This technical deep dive synthesizes recent work on the phenomenon of "grokking" in deep neural networks. Grokking refers to the abrupt transition from memorization to generalization during extended training on small datasets. The authors propose a geometric account of grokking centered on the dynamics of loss-landscape curvature, and systematically investigate this framework on two structurally distinct sequence-learning tasks: the SCAN compositional generalization benchmark and the Dyck-1 language depth prediction problem.

Problem & Context

• Grokking challenges conventional views of generalization, as standard training metrics provide no advance warning of the transition.
• Recent work has linked grokking to prolonged confinement on low-dimensional "execution manifolds" in weight space, followed by a sudden escape into a generalizing solution.
• A key open question is whether this geometric mechanism extends beyond the modular arithmetic tasks where it was first observed.

Methodology

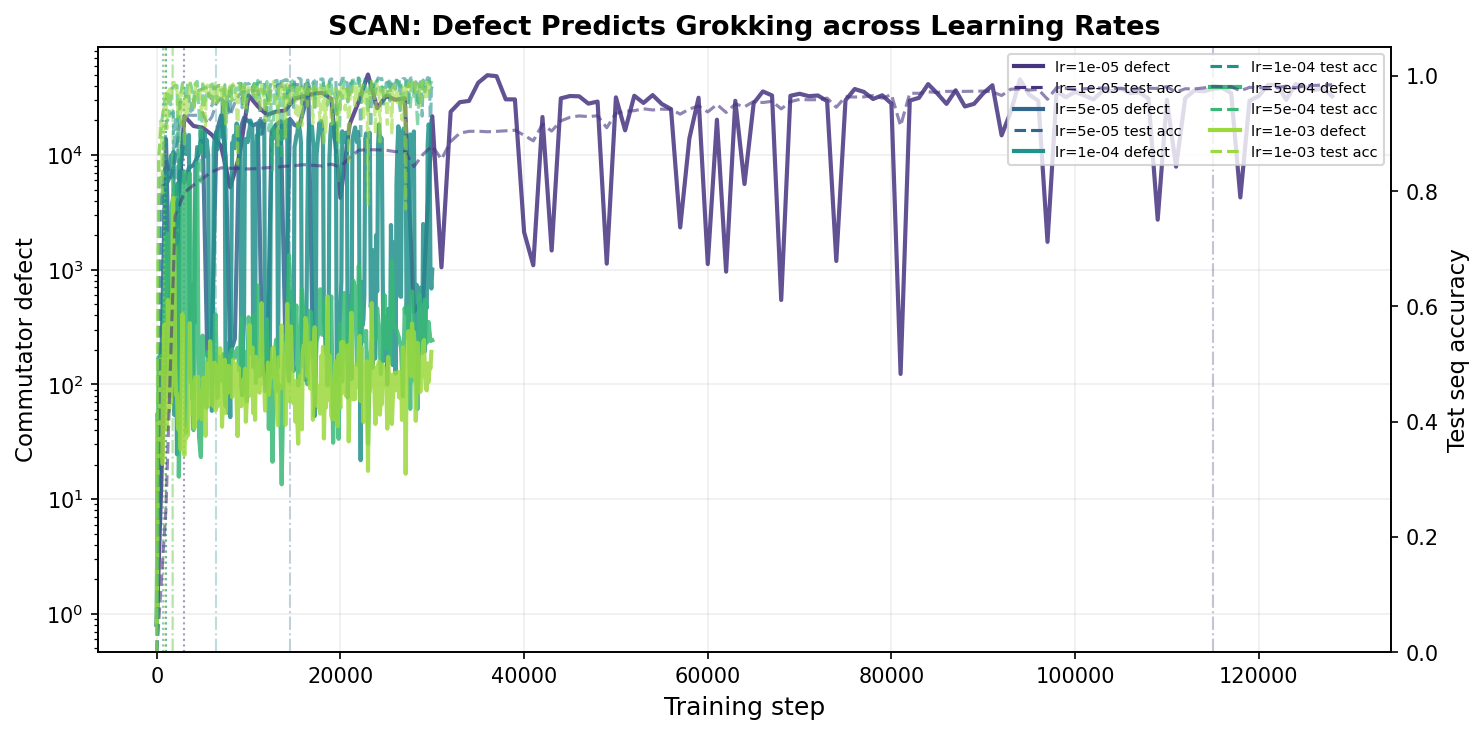
• The authors extend their prior analysis of the "commutator defect" — a measure of loss-landscape curvature — to SCAN and Dyck-1, which differ from modular arithmetic in architecture, input domain, output type, and dataset size.
• They analyze the scaling relationship between defect onset and the grokking timescale, compute PCA eigenspectra, and perform a three-basis "integrability decomposition" to understand the curvature dynamics.
• Causal intervention experiments test the role of the commutator defect in driving the grokking transition.

Data & Experimental Setup

• SCAN: Encoder-decoder transformer trained on 2,048 language-action pairs, tested on ~9,000 held-out examples.
• Dyck-1: Causal (decoder-only) transformer trained on just 50 parenthesis sequences, tested on 5,000.
• Both tasks use AdamW optimization, strong weight decay (λ = 1.0), and learning rate sweeps spanning two orders of magnitude.

Results

• On both SCAN and Dyck-1, the commutator defect spikes before the grokking transition, with a lead time following a super-linear power law (α ≈ 1.18 for SCAN, 1.13 for Dyck).
• At the slowest learning rates, the defect fires within the first 3-5% of training, providing 95-97% advance warning of grokking.
• The integrability decomposition shows the defect spike reflects structured non-commutativity within the learning subspace, specific to the grokking regime.
• Causal interventions confirm the defect's mechanistic role: boosting it accelerates grokking (by ~32% on SCAN, ~50% on Dyck), while suppressing orthogonal gradient flow delays or prevents it.

Interpretation

• The results extend the authors' prior geometric framework for grokking, confirming prolonged confinement on a low-dimensional manifold, curvature accumulation in transverse directions, and an escape into generalization.
• The commutator defect emerges as a fundamental, architecture-agnostic diagnostic of this process, outperforming spectral concentration as an early-warning signal.
• The three tasks exhibit a spectrum of causal sensitivity to curvature interventions, suggesting the accessibility of the generalizing solution may mediate the sufficiency of curvature boosting.

Limitations & Uncertainties

• Limited seeds at extreme learning rates, with only 1 seed each for the slowest SCAN and Dyck-1 settings.
• Single weight decay setting tested (λ = 1.0); impact of regularization strength on the scaling law exponent is unknown.
• Small model sizes (2-3 layers, 128-256 dimensions); behavior in larger transformers is untested.
• Synthetic tasks only; extending to natural language tasks is an important direction.

What Comes Next

• Investigating the correlation between solution complexity, causal sensitivity, and the geometric properties of grokking.
• Testing whether defect dynamics persist in billion-parameter language models.
• Exploring the instability regime observed at high learning rates on Dyck-1, and refining the grokking detection criteria.
• Integrating these geometric insights with other perspectives on the memorization-to-generalization transition, such as implicit bias and progress measure approaches.