Story
Position: Why a Dynamical Systems Perspective is Needed to Advance Time Series Modeling
Key takeaway
Advances in time series modeling by adopting dynamical systems theory could help improve forecasting and decision-making in areas like weather, finance, and medicine.
Quick Explainer
The core idea is to leverage insights from dynamical systems (DS) theory to advance time series (TS) modeling. DS theory provides a principled framework for understanding the underlying mechanisms that generate observed TS data, often originating from complex, chaotic systems. Dynamical systems reconstruction (DSR) models can infer surrogate models of these underlying dynamics directly from data, yielding benefits over traditional TS models in capturing long-term statistical properties and even outperforming them in short-term prediction on some datasets. This approach is distinctive in its grounding in fundamental DS principles, which enables simpler model architectures and training procedures compared to sophisticated TS models while still achieving strong empirical performance.
Deep Dive
Position: Why a Dynamical Systems Perspective is Needed to Advance Time Series Modeling
Overview
- Time series (TS) modeling has progressed from early statistical approaches to recent foundation models, but there are limitations in current methods
- The authors argue that adopting a dynamical systems (DS) perspective can significantly advance TS forecasting and analysis
Problem & Context
- TS of observations from natural or engineered systems almost always originate from some underlying DS
- Access to the governing equations of the underlying DS would yield theoretically optimal TS forecasts
- DS theory provides domain-independent insights into mechanisms underlying TS generation, enabling better forecasting and control
Methodology
- Review key concepts in DS theory and DS reconstruction (DSR), a class of ML/AI approaches that infer surrogate models of the underlying DS from data
- Discuss how insights from DS theory and DSR can inform and improve TS modeling
Data & Experimental Setup
- Comparisons of SOTA custom-trained DSR and TS models, as well as TS and DSR foundation models, on real-world datasets including energy, weather, traffic, and physiological signals
Results
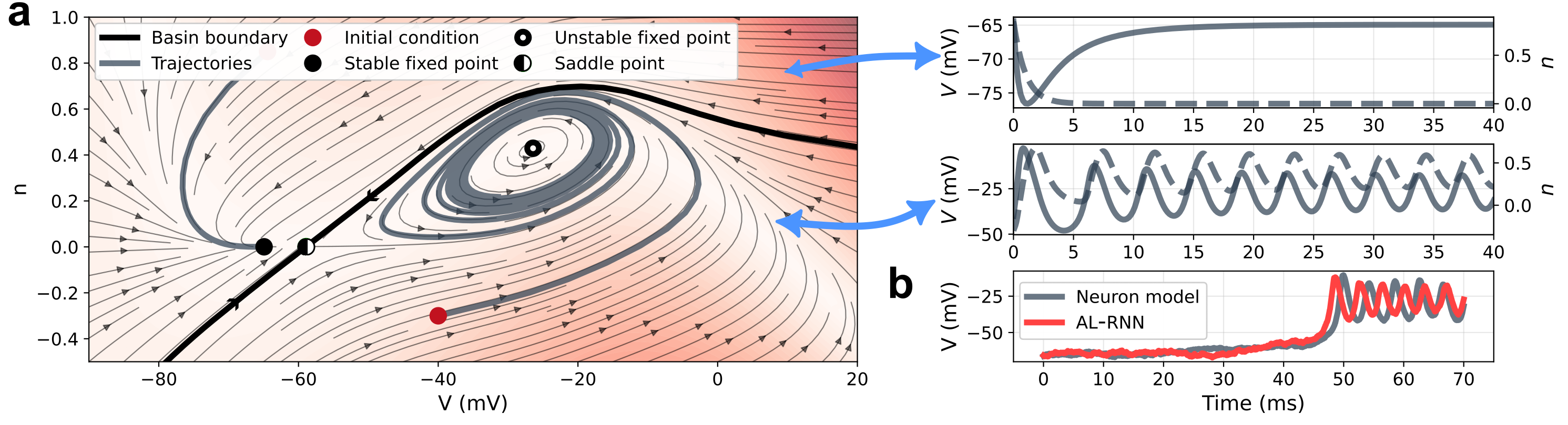
- DSR models outperform TS models in reproducing long-term statistical properties of chaotic systems
- Surprisingly, DSR models can also outperform TS models in short-term prediction on some datasets
- DSR models achieve comparable performance to sophisticated TS models despite simpler architectural design and lower training costs
Interpretation
- The training algorithms used, not just the network architecture, are critical for DSR performance
- DSR models may benefit from a more natural, chaotic training corpus and a more compact, DS-inspired model design
- DSR models show promise in predicting tipping points and abrupt regime shifts in underlying dynamics
Limitations & Uncertainties
- Most DS theory deals with low-dimensional, deterministic, autonomous systems, which may limit its applicability to many real-world TS
- However, extensions to stochastic and non-autonomous DS exist, and DSR models have been successfully applied to high-dimensional, complex, noisy empirical data
What Comes Next
- The authors provide specific recommendations for advancing TS modeling using DS principles:
- Incorporate DS-inspired training algorithms and loss functions
- Leverage DS-based measures to evaluate model performance
- Explore DSR models for predicting tipping points and extrapolating post-transition dynamics
- Integrate DSR models with LLMs to combine DS insights with external context knowledge