Outer Diversity of Structured Domains

Technical Deep Dive: Outer Diversity of Structured Domains

Overview

This technical deep-dive briefing summarizes the key findings from the paper "Outer Diversity of Structured Domains" (arXiv preprint). The work introduces a new measure of diversity for preference order domains, called "outer diversity", and analyzes the diversity of several well-known structured domains in voting theory.

Problem & Context

• In the standard ordinal model of elections, voters provide ranked preferences over a set of candidates.
• Some rankings appear more "rational" or natural than others, leading to the study of "structured domains" - subsets of the full preference order space that capture different notions of rational behavior.
• Examples of structured domains include single-peaked, single-crossing, and group-separable preferences.
• Prior work has proposed measures of domain diversity, including "richness diversity" and "inner diversity", but the authors introduce a new notion of "outer diversity" as an alternative.

Methodology

• The key idea behind outer diversity is to measure how spread out a domain's rankings are within the full space of all possible rankings, rather than focusing on the internal structure of the domain itself.
• Outer diversity is defined as the expected swap distance between a randomly sampled ranking and the closest ranking in the domain, normalized to be between 0 and 1.
• The authors provide efficient algorithms for computing outer diversity for various structured domains, including single-peaked, single-crossing, group-separable, and Euclidean domains.

Results

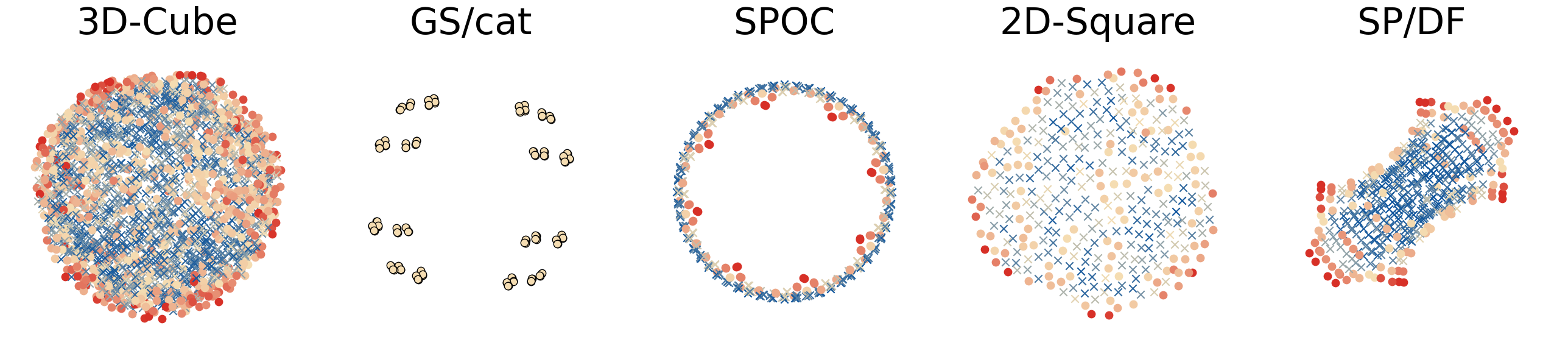
• Analyzing outer diversity for 8 candidate elections:
  • The group-separable domain based on caterpillar trees (GS/cat) and the 3D Euclidean domain are the most diverse.
  • The single-crossing (SC) and 1D Euclidean (1D-Int.) domains are the least diverse.
  • The rankings within group-separable domains (GS/bal, GS/cat) have uniform popularity, while other domains show more variance.
• Outer diversity generally decreases as the number of candidates increases, but GS/cat remains the most diverse for 12 or more candidates.
• Domains with exponential size (like GS/cat) maintain non-zero outer diversity as the number of candidates grows, while polynomial-sized domains (like SC, 2D-Square) see their diversity drop to near-zero.

Limitations & Uncertainties

• The algorithms for computing outer diversity have varying time complexities, with some requiring solving NP-hard problems for certain domains.
• The analysis is limited to up to 20 candidates, and the behavior for larger numbers is not explored.
• The relationship between outer diversity and other notions of diversity, like inner diversity, is not fully formalized.

What Comes Next

• Investigating the theoretical properties and limits of outer diversity as a measure of domain diversity.
• Extending the analysis to larger numbers of candidates and exploring the convergence properties of outer diversity.
• Establishing formal connections between outer diversity and other diversity measures used in computational social choice.