Low-Dimensional and Transversely Curved Optimization Dynamics in Grokking

Technical Deep Dive: Low-Dimensional and Transversely Curved Optimization Dynamics in Grokking

Overview

This paper proposes a geometric account of the "grokking" phenomenon, where neural networks trained on small datasets first memorize the training set and then, long after achieving perfect training accuracy, suddenly generalize to the test set. The key findings are:

• The weight-space trajectory during grokking lies on a low-dimensional, rank-1 submanifold (the "execution manifold") that exhibits empirical invariance under the optimization dynamics.
• Loss-landscape curvature, as measured by commutator defects, explodes orthogonally to this learned submanifold during grokking.
• This curvature growth consistently precedes the generalization transition by 600-1600 training steps, though it is a necessary but not sufficient condition.
• Causal intervention experiments confirm that suppressing motion along the execution manifold prevents grokking, while artificially inducing curvature is not sufficient.
• These findings hold across a wide range of hyperparameter settings, including a 200x difference in training timescale.

Methodology

• The authors use a Transformer model trained on modular arithmetic tasks (e.g. $(a+b) \mod 97$).
• They log the attention weight matrices during training and perform PCA analysis to identify the low-dimensional "execution manifold".
• They measure loss-landscape curvature using commutator defects, which quantify the non-commutativity of successive gradient steps.
• They project the commutator defects onto the PCA subspace to determine whether curvature is confined to the normal bundle.
• They conduct causal intervention experiments by suppressing gradient flow along the PCA directions or artificially inducing curvature.

Results

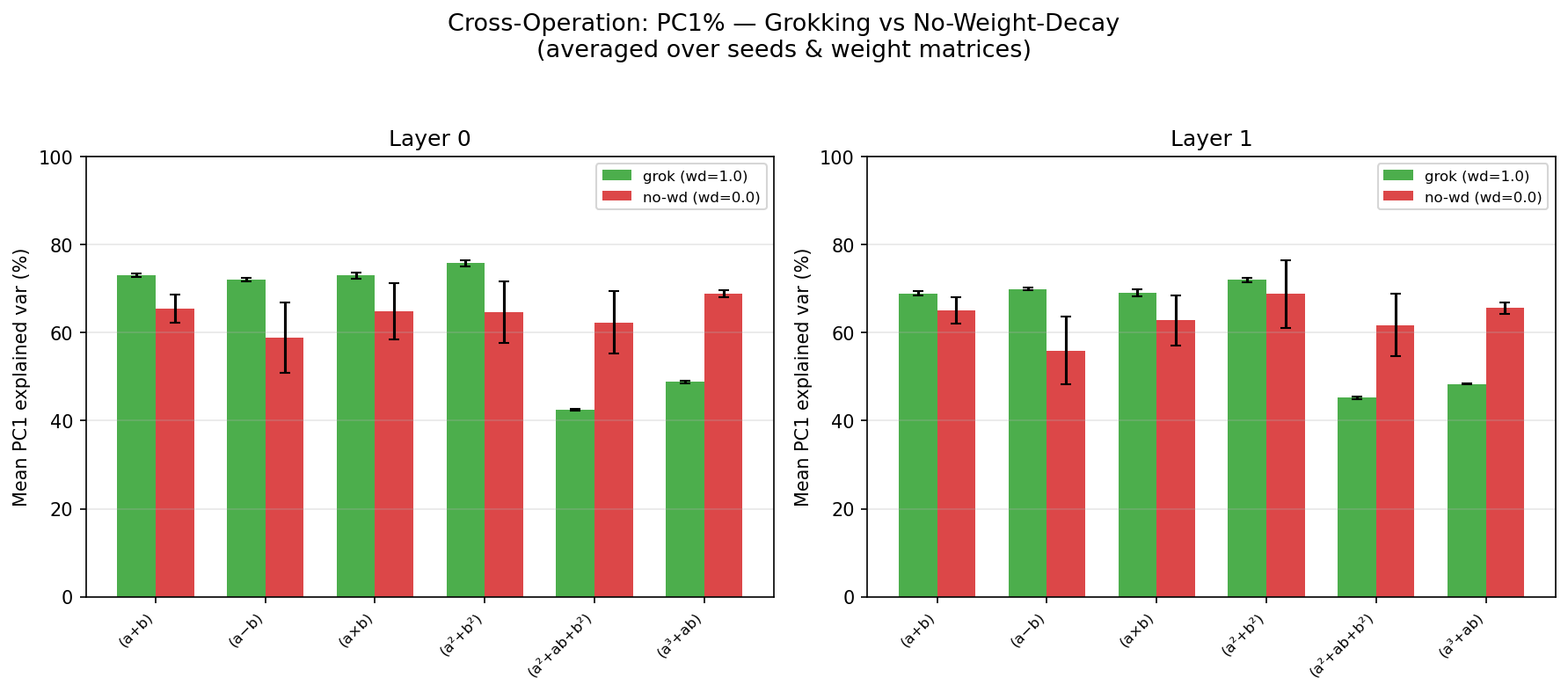
Rank-1 Execution Manifold

• PCA analysis reveals that a single principal component (PC1) captures 68-83% of the variance in the attention weight trajectories during grokking.
• This indicates the weight-space trajectory is confined to a low-dimensional, rank-1 submanifold.

Empirical Invariance of the Execution Manifold

• The commutator defects are predominantly orthogonal to the PCA subspace, with a residual fraction $\rho \approx 1.000$ across all conditions.
• This means the optimization dynamics are "transversely decoupled" - curvature is confined to the normal bundle and does not deflect the trajectory out of the learned subspace.

Orthogonal Curvature Explosion Precedes Generalization

• Grokking operations show a 10-1000x increase in commutator defect relative to non-grokking controls.
• The onset of this curvature growth consistently precedes the generalization transition by 600-1600 training steps.
• However, non-grokking operations also exhibit moderate curvature growth without generalizing, so the onset is a necessary but not sufficient condition.

Causal Interventions

• Suppressing gradient flow along the PCA directions prevents grokking with a monotonic dose-response, confirming the necessity of motion along the execution manifold.
• Artificially inducing curvature through directional forcing has no effect on the generalization transition, confirming that curvature growth alone is not sufficient.

Regime Invariance

• All findings replicate across a 200x difference in training timescale, as well as variations in learning rate, weight decay, and number of layers.

Interpretation

The authors propose that grokking reflects a geometric reorganization of the optimization landscape, governed by the interplay of curvature, damping, and the emergence of low-dimensional structure. Specifically:

• The weight-space trajectory becomes confined to a low-dimensional "execution manifold" during memorization.
• Curvature accumulates orthogonally to this manifold, creating a transverse instability.
• Generalization corresponds to the trajectory escaping this metastable regime, driven by a combination of curvature growth and regularization pressure.
• The learning rate controls the damping regime, with slower rates producing overdamped dynamics and larger predictive windows for the curvature onset.

This geometric picture unifies the empirical observations (rank-1 manifold, orthogonal curvature, predictive lead time, causal asymmetry) into a coherent dynamical narrative, drawing parallels to metastable escape in classical dissipative systems.

Limitations & Uncertainties

• The experiments are limited to relatively small Transformer models (2-3 layers, ~290k parameters) and synthetic algorithmic tasks (modular arithmetic).
• It remains unclear how well the observed phenomena generalize to large-scale language models and real-world datasets.
• Some of the geometric diagnostics (commutator defects, trajectory-curvature alignment) are computationally expensive and difficult to scale.
• A complete theoretical characterization of the observed phase transitions remains an open problem.

Future Work

• Investigate whether similar low-dimensional confinement and transverse curvature dynamics arise in other domains beyond modular arithmetic, such as Dyck languages and the SCAN benchmark.
• Develop efficient approximations and proxies for the expensive geometric diagnostics.
• Derive analytical models that capture the defect accumulation, manifold formation, and damping-controlled dynamics observed in the experiments.
• Explore how local curvature dynamics interact with global landscape structure to produce the grokking transition.