GREAT-EER: Graph Edge Attention Network for Emergency Evacuation Responses

Technical Deep Dive: GREAT-EER: Graph Edge Attention Network for Emergency Evacuation Responses

Overview

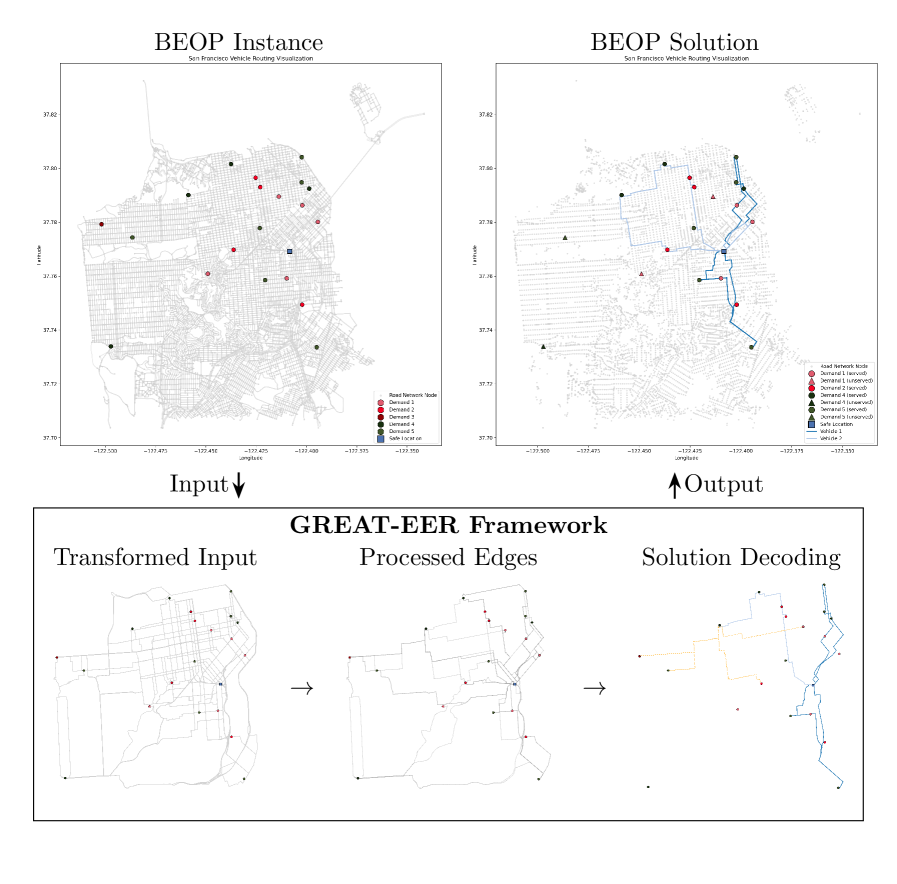
GREAT-EER is a deep reinforcement learning framework that solves the Bus Evacuation Orienteering Problem (BEOP) - an NP-hard combinatorial optimization problem for evacuating as many people as possible from an urban area using a limited number of buses within a fixed time window.

Problem & Context

• Emergency situations like wildfires, landslides, and volcanic eruptions are becoming more frequent due to climate change. Effective and fast evacuation strategies are critical.
• Purely car-based evacuations can lead to severe congestion and disorder, as seen during Hurricane Irma. Bus-based collective evacuation can help mitigate these issues.
• The BEOP problem aims to route a fleet of buses to pick up as many evacuees as possible from their locations, subject to capacity and time constraints. It is a variant of the Capacitated Team Orienteering Problem.
• The BEOP is NP-hard, so finding optimal solutions is computationally challenging, especially for large-scale real-world instances.

Methodology

Problem Formulation

• The BEOP is defined on a graph with nodes representing evacuation locations and a central depot. Edges have associated travel times.
• Each node has a prize (number of evacuees) and demand (space required on the bus).
• Buses have limited capacity and must return to the depot within a maximum evacuation time.
• Some nodes may have individual time windows for pickup.
• The objective is to maximize the total number of evacuees transported to the depot.

Solution Approach

• The GREAT-EER framework uses a graph neural network encoder (GREAT) to process the BEOP graph and an attention-based pointer network decoder to iteratively construct evacuation routes.
• The framework is trained end-to-end using reinforcement learning, without requiring an oracle solver for supervision.
• The POMO technique is used to improve robustness by exploring diverse solution rollouts during training.

Data & Experimental Setup

• Experiments use a real-world dataset of San Francisco's road network and point-of-interest data to generate realistic BEOP instances.
• Training and evaluation is done on instances with 100 evacuation nodes. Additional testing is performed on larger 200-node instances and instances with "hazard zones" where parts of the road network are blocked.
• The model is compared to an MILP solver (Gurobi) and a simple greedy heuristic baseline.

Results

• On small 20-node instances, GREAT-EER achieves near-optimal performance, outperforming the greedy baseline and matching the quality of the Gurobi MILP solver.
• On larger 100-node instances, GREAT-EER significantly outperforms the greedy heuristic, evacuating up to 94.41% of people compared to 85.53% for greedy.
• Using GREAT-EER's solution as a warm start greatly improves the Gurobi solver's performance, reducing the runtime from 24 hours to 10 minutes.
• GREAT-EER also performs well on out-of-distribution instances, maintaining a significant advantage over the greedy baseline.
• In a stochastic setting with uncertain travel times and evacuee demand, the dynamic, online version of GREAT-EER avoids invalid solutions and outperforms the deterministic variant.

Interpretation

• GREAT-EER demonstrates the effectiveness of using graph neural networks and reinforcement learning to tackle complex, real-world combinatorial optimization problems like the BEOP.
• The framework's fast inference speed (~1 second per 100-node instance) enables its use for real-time evacuation planning and resource optimization.
• The model's strong generalization abilities allow it to handle larger instances and adapt to unforeseen scenarios like hazard zones, making it a robust tool for emergency preparedness.

Limitations & Uncertainties

• The current BEOP formulation does not include all real-world factors, such as loading times, heterogeneous bus capacities, or prioritized evacuee groups.
• While GREAT-EER performs well on 200-node instances, scaling to even larger problem sizes remains an open challenge.
• The stochastic setting considered here is limited to uncertain travel times and evacuee demand. More elaborate dynamic changes (e.g., congestion, new evacuation nodes) could be explored in future work.

What Comes Next

• Extending the BEOP model and GREAT-EER framework to incorporate additional real-world constraints and objectives.
• Investigating methods to further scale the approach to handle larger problem instances.
• Exploring the integration of GREAT-EER into end-to-end emergency response systems, enabling rapid adaptation to dynamic, stochastic conditions.